Mathcamp 2001 Quiz

2001 Qualifying Quiz

You may also be interested in the printable (PDF) format or the LaTeX source code.

1.

In a certain game, there are three piles of stones: the first pile has 22 stones, the second pile has 14 stones, and the third pile has 12 stones. At each turn, a player may double the number of stones in a pile by transferring stones to it from one other pile. (For example, one could move 12 stones from the first pile to the third pile.) The game ends if the three piles all have the same size. Can you find a way to end the game in three moves?

2.

Suppose you randomly pick two different integers between 1 and 1,000,000. Is their sum more likely to be even or odd?

3.

Show that there are no positive integers m and n such that m(m+1) = n(n+2).

4.

Five mathematically gifted pirates, named Angry, Boorish, Crummy, Dirty, and Evil, must divide a loot of 100 gold doubloons. According to pirate law, Angry, the leader, can distribute the coins as she sees fit. However, when she is done, all five pirates (including Angry herself) take a vote: if more than half of them are unhappy with the distribution, Angry has to walk the plank (leaving her share of gold behind). The remaining four pirates, with Boorish as their new leader, then repeat the process: Boorish divides the loot, they all vote, and if more than half are unhappy then Boorish is done away with and Crummy takes charge of the gang. This process continues until the treasure is successfully distributed.

(a): How should Angry divide the money to ensure herself as large a share of the loot as possible? (You may assume that every pirate completely understands the strategy behind this process, and will always vote in such a way as to maximize his or her share. Furthermore, each pirate is bloodthirsty, and will vote to kill the current leader if it won't decrease his or her ultimate share of the loot or chances of survival.)
(b): What happens when there are more than five pirates? More than two hundred pirates?

5.

Aytek the Ant is standing at the point (0,10) in the x-y plane. Aytek is going to travel to the point (20,14), but in doing so, he must first travel to the x-axis - where much-needed sugar can be found - and walk along it for exactly 10 units. What route should Aytek take, in order to complete the whole trip from (0,10) to (20,14) in as short a distance as possible?

6.

If S_n denotes the sum of the decimal digits of the number 2ⁿ, either show that S_n does not equal S_n+1 for all positive integers n, or find a counterexample.

7.

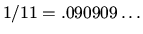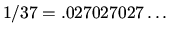The decimal expansion of the fraction $1/11 = .090909\ldots$ consists of the two digits 09 repeating over and over; we say that this decimal expansion has period length 2. Similarly, the decimal expansion of $1/37 = .027027027\ldots$ has period length 3. Can you find other integers n such that the decimal expansion of 1/n has period length 2? period length 3? Can you find all prime numbers p such that the decimal expansion of 1/p has period length at most 6? Can you find any prime numbers p so that the octal (i.e., base 8) expansion of 1/p has period length 3?

8.

Suppose a, b, c, and d are the side lengths of a quadrilateral with area S.

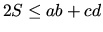(a): Show that $2S \le ab + cd$ .
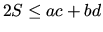(b): Show that $2S \le ac + bd$ .
(c): If either one of these two inequalities is in fact an equality, show that the quadrilateral can be inscribed in a circle.

9.

Suppose n disks, black on one side and white on the other, are laid out in a straight line with a random arrangement of black sides up. You are playing a game of solitaire, in which a turn consists of removing a black disk and flipping over its immediate neighbors, if any. (Two disks are not considered immediate neighbors if there used to be a disk between them that is now gone.) You win if you succeed in removing all n disks. Describe all initial configurations of disks that are winnable, explain how to win them, and show that all other configurations are unwinnable.

10.

Inside a 1 m by 1 m square box in the xy-plane, there are finitely many line segments, whose lengths sum to exactly 10 m. Show that there exists a straight line in the plane which crosses at least six of these line segments. (Hint: first, show that there exists a straight line in the plane which crosses at least five of these line segments.)