Mathcamp 1999 Quiz

1999 Qualifying Quiz

You may also be interested in the printable (PDF) format or the LaTeX source code.

Section A

1.: Show that there are no positive integers m and n such that m(m+1)=n(n+2).
2.: Find the smallest positive integer n such that 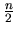is the square of an integer, 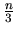is the cube of an integer, 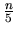is the fifth power of an integer, and 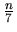is the seventh power of an integer.
3.: A triangle has sides of length a, b and c, which satisfy the equation 1/(a+b) + 1/(a+c) = 3/(a+b+c). Determine the angle opposite the side of length a.
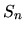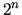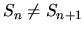4.: If is the sum of the decimal digits of the number , either show that $S_n is not equal to S_{n+1}$ for all positive integers n, or find a counterexample.
5.: I want to make a square lawn in the middle of a desert. For irrigation, I'll use two sprinklers, each of which can reach a circular area of radius 5 yards. The water from the sprinklers must cover the entire lawn. How large can my lawn be?
6.: (Extra Credit) A polynomial P(x) is said to be boring if it takes rational values for rational x and irrational values for irrational x. Prove that all boring polynomials are linear.

Section B

7.

Five mathematically gifted pirates, named Angry, Boorish, Crummy, Dirty, and Evil, must divide a loot of 100 gold doubloons. According to pirate law, Angry, the leader, can distribute the coins as she sees fit. However, when she is done, all five pirates (including Angry herself) take a vote: if more than half of them are unhappy with the distribution, Angry has to walk the plank (leaving her share of gold behind). The remaining four pirates, with Boorish as their new leader, then repeat the process: Boorish divides the loot, they all vote, and if more than half are unhappy then Boorish is done away with and Crummy takes charge of the gang. This process continues until the treasure is successfully distributed.

(a): How should Angry divide the money to ensure herself as large a share of the loot as possible? (You may assume that every pirate completely understands the strategy behind this process, and will always vote in such a way as to maximize his or her share. Furthermore, each pirate is bloodthirsty, and will vote to kill the current leader if it won't decrease his or her ultimate share of the loot.)
(b): What happens when there are more than five pirates?

8.

Three bugs are crawling on the coordinate plane. They move one at a time, and each bug crawls in a direction parallel to the line joining the other two.

(a): If the bugs start out at (0,0), (3,0), and (0,3), is it possible that after some time the first bug will end up back where it started, while the other two switch places?
(b): Can the three bugs end up at (1,2), (2,5), and (-2,3)?

9.

You are a secret agent assigned to carry out classified research on the C_n-tower, an ultra-modern office block n stories tall. Your mission: to determine the highest floor of the building from which a dropped egg will survive falling to the ground. Your equipment: a supply of exactly k eggs.

(a): Suppose k=1: you have only one egg (and once it smashes, that's it). How can you determine the highest floor that is safe? Are there any other strategies?
(b): Suppose k=2. You need to complete your mission as quickly as possible. What strategy should you use to determine the safe height efficiently? (Here ``efficiently'' means that the worst case scenario takes as few test drops as possible.)
(c): Can you find an answer for higher values of k?

10.

It is a well-known fact that

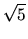is not rational (i.e. cannot be written as a fraction p/q for integers p and q).

(a)

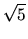does crop up very naturally in geometry. Draw a picture to illustrate this.

(b)

We could try to write

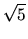as a ``continued fraction'':

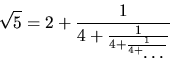
sqrt{5} = 2 + 1 / (4 + 1 / (4 + 1 / (4 + ... )))

What might we mean by this?

(c)

Alternatively, we can look for rational numbers that are approximately equal to

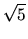. Let

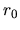be a positive rational number close to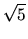

. Show that

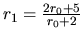is even closer to

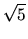(d)

Suppose we let

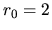, and repeat the procedure of (c) by setting 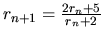$r_{n+1} = (2*r_n+5)/(r_n+2)$ . Can you see a connection between the sequence of numbers

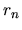and the continued fraction in part (b)? Can you prove it?

11.

A polygon with n sides is called an n-gon. Here n is assumed to be a positive integer, but we can also define fractional polygons, or

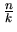-gons. To draw a regular

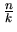-gon, start with any vertex of a regular n-gon, and label it 1. Count off k vertices clockwise, and label the vertex you end on 2. Count off k more vertices and label that vertex 3. Continue in this way until you get back to 1. Now draw an edge from 1 to 2, from 2 to 3, etc., and from the last vertex back to 1. (Notice that in fractional polygons, edges are allowed to intersect.) For example, a

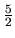-gon is a five-pointed star; we still think of it as having 5 vertices and 5 edges.

(a): Experiment with different values of n and k. How many vertices does an 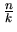-gon have? When do different values of n and k produce the same polygon?
(b): How many different regular 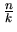-gons with n vertices are there? (Try it first for n = prime.)

Projects

P1

Polyominoes (also called n-ominoes) are made by sticking n square tiles together by their edges, in flat configurations. For example, the blocks in the game Tetris form a complete set of 4-ominoes. We will consider mirror images to be the same, so there are exactly five (different) 4-ominoes.

(a): There are exactly two 3-ominoes. The T-shaped 4-omino can be placed on each of them, covering them completely. Can you find a 6-omino that covers all the 4-ominoes? Show that there is no 5-omino that can cover all the 4-ominoes.
(b): How many 5-ominoes are there? Find a k-omino that can cover all the 5-ominoes. How small can k be?
(c): Is it true that for all values of n, there is a 2n-omino that covers all n-ominoes?
(d): Let f(n) be the size of the smallest polyomino that can cover all n-ominoes. What can you say about f(n)? For example, what are the best upper and lower bounds for f(n) that you can give? [You are NOT expected to look for an exact general formula.]

P2

If you have Internet access, take a look at the website ``Clever Games for Clever People'', at:

http://www.cs.uidaho.edu/~casey931/conway/games.html

See if you can find a winning strategy (or partial strategy) for one or more of the games described there, and tell us about it.

P3

This problem is about even and odd numbers in Pascal's triangle and, believe it or not, fractals!

(a): On a piece of graph paper, write down the first 5 or 6 rows of Pascal's triangle, putting one number in each square. (You may want to orient the paper diagonally.) Now color each square that contains an even number black, and each square that contains an odd number red. Extend this coloring to 10 or 15 more rows of the triangle. (Do you have to compute the actual numbers to do this?) Describe the pattern that you see, and try to predict how it continues.
(b): Assuming your pattern is correct, what fraction of the numbers in Pascal's triangle are even? (Before you even try to answer this question, think about what it could possibly mean. After all, the triangle is infinite!)
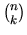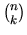(c): As you probably know, the k^th entry in the n^th row of Pascal's triangle (if we start the numbering from 0) is the binomial coefficient . (Can you prove this?) Write n and k in binary, and see if this helps you predict whether will be even or odd. Is this the same pattern that you found before? Can you prove it this time?
(d): In fact, there is a general formula for the divisibility of binomial coefficients by prime numbers. It's tricky, but give it a try: draw pictures, try different bases, formulate conjectures, and see if you can prove them.