2017 Qualifying Quiz
You may also be interested in the printable (PDF) format or the LaTeX source code.
-
Lotta is a consulting mathematician who specializes in very large numbers. She runs a business with 100 clients ranked 1 through 100 in order of importance. (The most important client is ranked 1.) Each day, Lotta has time to visit only one of her clients.
A client feels mistreated if Lotta has never visited them, or if Lotta has visited someone less important since the last time she visited them. Every day, Lotta visits the most important client that feels mistreated. On the first day, she visits client 1; on the second day, she visits client 2; on the third day, she goes back to client 1, and so on.
When none of Lotta's clients feel mistreated, she can finally retire.
- Prove that Lotta will be able to retire someday.
- Over the course of Lotta's career, how many days will the Nth client wake up feeling mistreated?
- Describe the set of people that wake up feeling mistreated on the Nth day.
-
This problem is about some curious relations between the sums of certain entries of Pascal's triangle. You may find the following background reading useful: Pascal's Triangle and Binomial Coefficients.
In this problem, we define
(
) = (n k mod m
) + (n k
) + (n k + m
) + ...n k + 2m where the sum includes every mth element between 0 and n inclusive, starting at k. For example,
(
) = (20 2 mod 5
) + (20 2
) + (20 7
) + (20 12
) .20 17 -
Find, with proof,
(
) and (n 0 mod 2
) . (This is a well-known result that you may have seen before; in that case, consider it a warm-up.)n 1 mod 2 -
Show that
(
) is always one of the two integers closest to 2n/3. For which values of n is it larger than 2n/3, and for which values of n is it smaller?n 0 mod 3 -
Let Dn be the difference between the largest and the smallest among the numbers
( Find Dn.
), (n 0 mod 5
), (n 1 mod 5
), (n 2 mod 5
), and (n 3 mod 5
).n 4 mod 5
-
Find, with proof,
(
-
It's the week before Mathcamp, and the N mentors are frantically preparing their classes. The Mathcamp library is open around the clock, and each mentor visits it once in every 24 hour period. They follow a strict schedule: each mentor has a set time when they enter the library and a set time when they leave. (Some mentors work through the night, arriving in the evening and leaving in the morning.) No mentor arrives or departs at the exact same time as another: all 2N times are different.
It so happens that:
- There are 47 pairs of distinct mentors that sometimes see each other in the library. (All other pairs of mentors visit the library at non-overlapping times.)
- One day, the mentors decide to estimate the typical number of mentors in the library. That day, each mentor writes down the number of other mentors in the library when they arrive and again when they leave (not counting themselves). The average of these 2N numbers is 4.
- Two of the mentors, Jane and Sam, are so dedicated that at any time of day or night, at least one of them is in the library. (They are the only pair of mentors with this property.)
- What is N, the number of mentors at Mathcamp?
- Suppose we vary A = 47 (the number of pairs of mentors that see each other), B = 4 (the average computed by the mentors), and C = 1 (the number of mentor pairs like Jane and Sam). Find an equation for N in terms of A, B, and C.
-
Let k be a positive integer, and let Ek be the equation
m(m + 1) = n(n + k). A solution to Ek is a pair of positive integers m and n that satisfy the equation. For example, solutions to E2017 include m = 3459, n = 2595 and m = 4484, n = 3588. (There are others as well.)
- For what positive integers k does Ek have no solutions? Be sure to prove your answer, including showing that Ek does have a solution for all other values of k.
- Find, with proof, the solutions to E2017 with the smallest and the largest possible values of m.
- Show that, with a few exceptions, it is impossible for both Ek and Ek+1 to have exactly one solution. What are the exceptions?
-
Wizards live in towers that have infinitely many floors, numbered 1, 2, 3, ... . The floors are not connected by staircases or any other mundane means. Instead, for every positive integer N, there is a red magic portal connecting floor N to floor N + 10, and a blue magic portal connecting floor N to floor 3N + 1. The portals go both ways; for example, starting at floor 26, you could descend to floor 16 by a red portal, descend to floor 5 by a blue portal, and ascend to floor 15 by a red portal.
Of course, an infinitely tall tower would have enough room for multiple wizards. But wizards refuse to share: two wizards refuse to both live in the tower if it's possible to get from one wizard's floor to the other wizard's floor using the magic portals.
- How many wizards could live together in such a tower?
- If the red portals instead connected floor N to floor 2N + 1, and the blue portals instead connected floor N to floor 8N + 1, how many wizards could live in the tower?
- If the red portals instead connected floor N to floor 2N + 1, and the blue portals instead connected floor N to floor 3N + 1, how many wizards could live in the tower?
-
(This problem first appeared on Mathcamp 2015's weekly Team Problem Solving competition.)
A triangle function assigns a nonnegative real number to all nondegenerate triangles. We call a triangle function f consistent if any two congruent triangles are assigned the same value: f(△ABC) = f(△DEF) whenever △ABC ≅ △DEF.
Suppose that for some △ABC, points X, Y, and Z are chosen in the interior of sides AB, AC, and BC, respectively. If a triangle function f satisfies
f(△AXY) + f(△BXZ) + f(△CYZ) = f(△ABC) for all choices of △ABC, X, Y, and Z, we say that f has the triforce property. (In the diagram below, the function's values for each of the shaded triangles must add up to the function's value for the large triangle.)
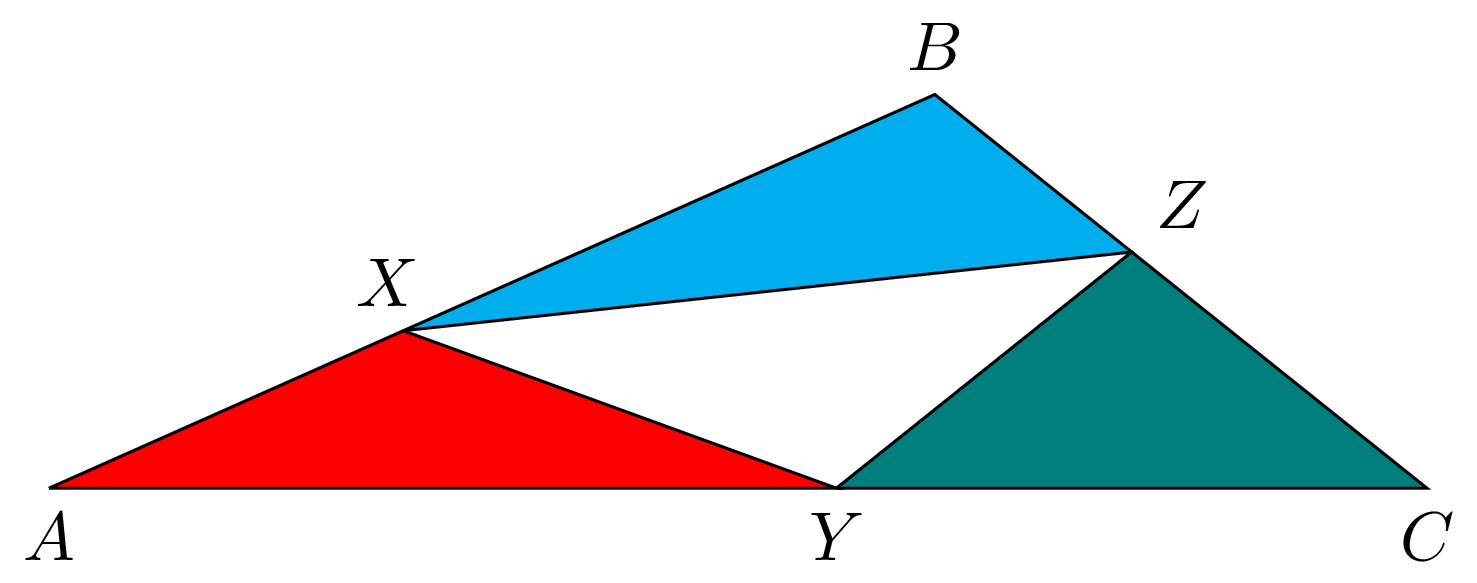
Figure 1: f's values at △AXY (red), △BXZ (cyan), and △CYZ (teal) must add up to f's value at △ABC.Is there a consistent triangle function with the triforce property, other than the trivial function assigning the value 0 to every triangle?
-
Waldo and Carmen play a guessing game played in N cities located on a large ring around the earth. Two cities that are next to each other in the ring are chosen uniformly at random. Waldo is sent to one of them and Carmen is sent to the other. Neither player knows which of the adjacent cities the other is in (but each knows her or his own location).
Starting with Waldo, the players take turns guessing where the other is. More precisely:
- A player can choose to name any of the N cities as their guess.
- Each player hears the other's guesses and can use that information when making future guesses.
- A player's guessing strategy can be probabilistic: they can decide to guess City 1 with probability p, City 2 with probability q, and so on.
- If N = 3, find a strategy for Waldo that wins him the game with probability at least 2/3, no matter what strategy Carmen uses.
- If N = 3, find a strategy for Carmen that wins her the game with probability at least 1/3, no matter what strategy Waldo uses.
- What are Waldo and Carmen's optimal strategies in the general case? (You might want to try N = 6 and N = 8 to begin with.)
Problem #1 is due to Bill Kuszmaul, MC '12–'13; problem #2 is due to Austin Shapiro, who teaches mathematics at Proof School in San Francisco; problem #5 is due to Drake Thomas, MC '14–'16; all other problems were written by the Mathcamp staff.





