2022 Qualifying Quiz

1. Define a "digital number" in base b (b > 1) to be a positive integer n such that the base-b digits of n² add up to n. For example, 9 is a digital number in base 10 because 9² = 81, and 8 + 1 = 9. Also, 9 is a digital number in base 7 because 9² = 81 is written as 144 in base 7, and 1 + 4 + 4 = 9.
   1. There are five other digital numbers in base 7, aside from 9. What are they?
   2. It is not a coincidence that base 7 = 2² + 2 + 1 has unusually many digital numbers. Prove that for all k ≥ 2, there are at least five digital numbers in base k² + k + 1.
   3. Find all integers b > 1 such that b + 3 is a digital number in base b. (Prove your answer!)
   4. Prove that in any base b ≥ 16, every digital number is less than b^3/2. What's the best upper bound you can prove on the largest digital number in base b, when b is large?
2. Figure 1a shows the 13^th stage of a fractal obtained by the following process. The 1^st stage is a single black square. The n^th stage is obtained by combining two congruent copies of the (n - 1)^th stage: one copy is rotated 90° counterclockwise and placed to the right of the other, so that they are aligned along the bottom side. An example of this is shown in Figure 1b.
   

   

   

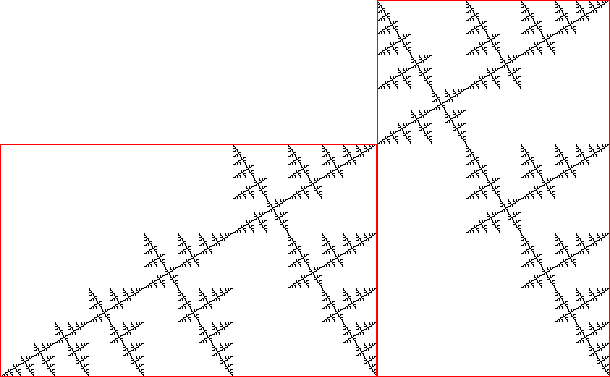
   1. As n increases, the slope of the diagonal line from the bottom left corner to the top right corner gets closer and closer to some value m. What is m?
   2. In the n^th stage, let a_n be the area of the black region above the diagonal line, and let b_n be the area of the black region below the diagonal line.
      As n increases, a_n / b_n gets closer and closer to some value a / b. What is a / b?
3. Marvin is playing a solitaire game with marbles. There are n bowls (for some positive integer n), and initially each bowl contains one marble. Each turn, Marvin may either
   • remove a marble from a bowl, or
   • choose a bowl A with at least one marble and a different bowl B with at least as many marbles as bowl A, and move one marble from bowl A to bowl B.
   The game ends when there are no marbles left, but Marvin wants to make it last as long as possible.
   1. Prove that the game must end after at most n(n+1)/2 turns.
   2. Prove that for every positive integer k, there is an n such that Marvin can make the n-bowl game last for at least kn turns.
   3. Marisa comes along and asks to join the game. Marvin and Marisa revise the rules: they will alternate taking turns, starting with Marisa. When the game ends, whoever took the last turn is the winner.
      Prove that among any three consecutive values of n, there is at least one value for which Marvin has a winning strategy.
4. An architect is designing a city. The city will be built on the segment of the x-axis from (0,0) to (1,0). Each building is a rectangle whose bottom edge rests on this segment of the x-axis. In the architect's vision, the city has infinitely many buildings: the n^th building to be built will have width (1/2)ⁿ and height n. Two buildings cannot overlap, but they can share a vertical edge.
   
   The sun rises in the east (in the positive x direction, to the right of the city). A building has a nice view if you can see the sunrise from the top floor: there are no taller buildings to its right blocking the view.
   
   There are also some parks in the city. You may have noticed that the widths of the buildings add up to 1, so there's no room to add parks. Therefore all the parks are very small: just single points on the x-axis. However, parks must still be outdoors: If a building's bottom edge runs from (a,0) to (b,0), we cannot add a park at any point (x,0) for a < x < b.
   1. Suppose that there is a park at the point (1/3, 0). Is it possible to design the city so that every building east of the park has a nice view? Can any buildings west of the park have a nice view?
   2. Suppose that there are two parks: one at (x₁, 0) and one at (x₂,0), with 0 < x₁ < x₂ < 1.
      For which x₁ and x₂ is it possible to design such a city? (No nice views are required.)
   3. For which x₁ and x₂ is it possible to design the city so that every building between the two parks has a nice view?
   4. Show that it's possible to design the city so that no building shares a vertical edge with any other building. Can any buildings in such a city have a nice view—and if so, how many? [NOTE: We have received many questions on the statement of this problem. Please see the FAQ for further clarifications.]
5. Assaf, Ben, Charlotte, Dan, and Emily are set to appear on the hit reality TV game show Singleton. At the end of each episode, one of the contestants is "voted out of the set" and eliminated from the game. The last contestant remaining wins.
   
   In the voting phase of the episode, each contestant left in the game casts a vote against another contestant still in the game. They vote one at a time, in alphabetical order. The votes are public: when a contestant goes to vote, they are aware of all votes cast so far, and can use that information to inform who they vote against. Once everyone has voted, the contestant that received the most votes is eliminated. If there is a tie, the player who is last alphabetically among those who received the maximum number of votes is eliminated.
   
   It is common knowledge that the contestants all act rationally according to the following priorities:
   1. A contestant's top priority is to avoid elimination for as many episodes as possible (in particular, they would like to win the game if possible).
   2. A contestant wants to eliminate someone in this episode that is as early in the alphabet as possible (without compromising the top priority of lasting as long as they can).
   1. Who gets eliminated in the first episode? Who wins the game?
   2. Suppose the game show begins with an immunity challenge. The winner of the challenge cannot be eliminated in the first episode; nobody is allowed to vote against them. If Dan wins the immunity challenge, who gets voted out? What if Emily wins instead? What if Assaf wins?
   3. Suppose the winner of the immunity challenge is allowed to give their immunity away to another contestant. Does it ever make sense for a contestant to choose to do so?
6. You are investigating a dangerous cult, with the goal of uncovering its reclusive Mastermind. From previously gathered intelligence, you know that the cult has 100 members: the Mastermind, the Go-between, the Figurehead, and 97 Pawns. Each member of the cult associates with some, but not all, of the other members. In particular:
   • The Mastermind is very reclusive; they associate with the Go-between, but no other member.
   • The Go-between associates with the Mastermind and the Figurehead, but none of the Pawns.
   • The Figurehead associates with everyone except the Mastermind.
   • The Pawns associate with the Figurehead, but not the Mastermind nor the Go-between. Some pairs of Pawns may also associate with each other (so, each Pawn could potentially have up to 97 total associations).
   You cannot figure out which members have special roles just by looking. However, each day, you can select a pair of members to investigate, and determine whether they associate with each other.
   1. Prove that if you investigate all pairs of members, then you can identify the Mastermind.
   2. Is there a strategy to find the Mastermind in under 1000 days?
   3. Suppose there are n members in the cult: one Mastermind, one Go-between, one Figurehead, and n - 3 Pawns. How quickly can you find the Mastermind?
      (We don't know the exact answer to (c), but we know some good bounds. Do your best!)

Problem #1 is due to Max Misterka (MC 2021). Problem #4 is due to Conrad Kosowsky (MC 2013–2014). Problems #2, #3, #5, and #6 were written by the Mathcamp staff. Problem #2 first appeared in Mathcamp 2021's weekly Team Problem Solving competition.

FAQ Answers

Many applicants asked us questions to clarify the statements of Quiz problems via our QQ helpline. Here are some of the questions and our answers; you might find them helpful!

Problem 1

Problem 3

Problem 4

Problem 5

Problem 6