2012 Qualifying Quiz

You may also be interested in the printable (PDF) format or the LaTeX source code.

  1. A frog jumps along the number line. It starts at 0 and every second it jumps n units to the right (the same positive integer n each time). After one second, you decide that you want to catch the frog. It's dark, you can't see the frog, and you don't know what n is. (For all you know, it might be a super-frog, so n could be arbitrarily large.) However, at any given second, you are allowed to choose an integer and search there. If the frog is on that integer, you'll catch it; if not, you'll have to try again.
    1. Devise a strategy that will eventually catch the frog. (You'll need to explain which integer you plan to check at each second.)
    2. Now suppose the frog is allowed to start by going either to the left or to the right; once it chooses a direction, it always jumps n units in that direction. Can you devise a strategy for catching it if you don't know which way it's going, and don't know what n is?
    3. What if the conditions in part (b) hold, and you also don't know which integer point the frog started at? (After you have worked on this problem for a while, it may be useful to read the following article, particularly the section after the proof of Lemma 1: Cut The Knot's "What is a number?".)
  2. Each integer on the number line is colored with exactly one of three possible colors—red, green or blue—according to the following two rules: the negative of a red number must be colored blue, and the sum of two blue numbers (not necessarily distinct) must be colored red.
    1. Show that the negative of a blue number must be colored red and the sum of two red numbers must be colored blue.
    2. Determine all possible colorings of the integers that satisfy these rules.
  3. Let p be an odd prime. A group of p campers sit around a circle, and are labeled with the integers 1,2,...,p in clockwise order. The camper with label 1 yells out the number 1. The camper sitting next to this camper in clockwise order yells out 2. The camper two spots in clockwise order from the camper who yelled out 2 yells out 3. This process continues: the camper seated n spots (in clockwise order) from the camper who yelled out n must yell out n+1. A camper gets a cookie anytime she or he yells out a number.
    1. Show that there is a camper who never gets a cookie.
    2. Of the campers who do get cookies, is there one who at some point has at least ten more cookies than the others?
    3. Of the campers who do get cookies, is there one who at some point has at least ten fewer cookies than the others?
  4. Let a be a rational number with 0 < a < 1. A lollipop in the xy-plane with base (a,0) consists of a line segment from (a,0) to some point (a,b) with b > 0, together with a filled in disc of radius less than b, centered at (a,b). Determine whether or not it is possible to have a set of lollipops in the xy-plane satisfying both of the following conditions:
    • for every rational number a with 0 < a < 1, there is a lollipop whose base is the point (a,0),
    • no two lollipops touch or overlap each other.
    If such a set of lollipops exists, explain how to construct it. If not, justify why not.
  5. A convex body in the plane is a region with positive area such that for any two points in this region, the entire line segment between them also lies within the region. Let P be the perimeter (i.e., boundary) of a convex body in the plane. We will assume throughout this problem that P is centrally symmetric: that is, if (a,b) is a point on P, then so is (-a,-b).

    For any nonnegative real number k, we define kP to be the subset of the plane obtained by multiplying all the points of P by k in each coordinate. In other words, for each point (a,b) of P, the point (ka,kb) is in kP.

    If (x1,y1), (x2,y2) are two points in the plane, we define the P-distance between them to be the smallest nonnegative real number k such that when the set kP is translated by (x1,y1) (that is, by x1 units horizontally and by y1 units vertically), the point (x2,y2) lies on it. For example, suppose that P is the square with vertices (0,1), (1,0), (0,-1), (-1,0); then the P-distance between (3,5) and (4,10) is 6.
    1. Let P be the perimeter of a disc of radius 1 centered at the origin. Find a formula for the P-distance between any two points (a,b) and (c,d) in the plane.
    2. Let P be the perimeter of a rhombus with vertices (2,0), (-2,0), (0,3), (0,-3). Find a formula for the P-distance between any two points (a,b) and (c,d) in the plane.
    3. In part (a), we took it for granted that a filled-in disc of radius 1 is a convex body. Prove this rigorously, using the definition of convexity given above.
    4. Suppose P is a convex quadrilateral. What are the possible P-distances between vertices of P? What about when P is a convex hexagon? (Remember: P must still be centrally symmetric!)
    5. Let P be the perimeter of some centrally symmetric convex body, and let (a,b) be a point on P. What is the largest possible P-distance from (a,b) to another point on P? Will (a,b) be at this P-distance from just one other point on P or from multiple other points? (If any of your answers depend on the geometry of P and/or on the choice of (a,b), explain how.)
    6. In principle, we could define P-distance even when P doesn't come from a convex body and/or is not centrally symmetric. But it turns out that in both of these cases, the definition is problematic: the resulting quantity doesn't behave in the ways we expect a "distance" to behave. Can you determine what problematic issues arise?
  6. An ocean has infinitely many islands. Every island is labeled by one of the integers ...,-3,-2,-1,0,1,2,3,..., with no two islands having the same label and every integer being the label of some island. Two islands are connected by a bridge if their labels differ by a power of two. For instance, there is a bridge connecting island 7 and island -25.

    We define the distance between two islands k1 and k2 to be the minimum number of bridges needed to get from k1 to k2. For instance, the distance between the islands 0 and 7 is 2. (You can move from island 0 to island 8, then to island 7; this is the minimum, since you can't go from 0 to 7 using just one bridge.)
    1. Show that for any integer r ≥ 1, you can find two islands in the ocean at distance r from each other.
    2. An infinite path in our ocean consists of an infinite set of islands I and an infinite set of bridges B, with each bridge in B joining two islands in the set I, such that:
      • every island in I is connected to exactly two bridges in B,
      • for any two islands in I, you can get from one to the other using only bridges in B.
      Here is one example of an infinite path: let I be the set of all odd-numbered islands and let B be the set of bridges between islands in I whose labels differ by 2. It is easy to see that I and B satisfy both conditions for an infinite path:
      • Each island k in I is connected to exactly two bridges in B – namely, the bridges leading to islands k-2 and k+2;
      • To get from any odd-numbered island to any other using bridges in B, you start at the smaller number and keep adding 2.
      As a warm-up, can you create an infinite path with the same I as in the example above, but with a different B?
    3. Is it possible to construct an infinite path in our ocean such that, for any two islands k1, k2 in I, the minimum number of bridges in B needed to get from k1 to k2 is exactly the distance between k1 and k2? For instance, the infinite path in our example does not have this property: it takes two bridges in B to go from island 1 to island 5 (you have to go via island 3), even though the distance between these two islands is 1 (there is a single bridge not in B that connects them to each other). If your answer is yes, give an example of sets I and B that work. If your answer is no, prove that it can't be done.
    4. Does there exist a set S of 9 islands such that:
      • the configuration of bridges connecting pairs of islands in S is exactly as in the picture below (with no additional bridges between any of the islands), and
      • the distance between any two islands in S equals the minimum number of bridges needed to get from one island to the other via islands in S?
      image of 3x3 lattice
      What if, instead of a 3x3 grid, we had an nxn grid: for which n is such a configuration possible?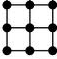
    5. Suppose, in a sea far away, we have islands labeled in the same way, with two islands connected by a bridge if their labels differ by a power of 3. Is there a one-to-one correspondence between islands in the ocean and islands in the far-away sea, such that two islands in the ocean are connected by a bridge precisely when the corresponding two islands in the sea are connected by a bridge?
  7. Last summer, the graduate students teaching at Mathcamp (we call them "mentors") arranged themselves into a pyramid with four layers:
    Photo of MC 2012 mentors in a 4-level pyramid
    Now suppose we generalize this to a pyramid with n layers (n mentors in the bottom row, n-1 mentors in the row above, etc.). Assume that all mentors have weight 1 and that each mentor supports their own weight plus half the weight supported by the one or two mentors leaning on them. For instance, in our four-layer mentor pyramid, the weights supported by the mentors are
    layer 1: 1
    layer 2: 3/2 3/2
    layer 3: 7/4 5/2 7/4
    layer 4: 15/8 25/8 25/8 15/8
    1. Find the weight supported by the mentor at the bottom left corner of a pyramid with n layers.
    2. Now suppose the pyramid has infinitely many layers. Let W(k,m) be the weight supported by the k+1-th mentor from the left in the m+1-th layer. For instance, W(0,0)=1, W(0,1)=W(1,1)=3/2, etc. Determine a recursive formula satisfied by the function W(k,m) for k,m ≥ 0.
    3. Find an explicit formula for W(k,2k) in terms of k, for k ≥ 0. If you can't find a fully explicit formula, can you find one that uses summation notation?
    4. Extra credit: What can you say about W(k,m) in general?
    Note: If you're not sure what we mean by "explicit" and "recursive" formulas, here is some helpful background reading.