The 2026 Quiz Problems

New this year: for each problem we are asking for your scratchwork and list of resources used. We strongly encourage you to make an account on our portal at appsys.mathcamp.org right away, and upload your scratchwork as you go. Read the Instructions!

If you haven't read it yet, read our policy on getting help on the Quiz. In brief: external resources can be used to learn background material, but not to find, write, or check solutions. (Our policy on getting help on other parts of the application is here.)

Do not ever post these problems in online forums. Good luck and have fun!

You may be interested in the printable format (.pdf). Handwritten solutions are welcome, but if you are typing your solutions you may find the LaTeX source code (.tex) helpful. You can find all the files necessary to compile this yourself, along with .tex solution templates for each problem, in this zip file. (You are not required to use these templates, however!)

1. A group of n people play a game where they all stand in a circle, each wearing a red or blue hat. In each round of the game, any player whose neighbors' hat colors match each other advances to the next round, while the players with one red-hat neighbor and one blue-hat neighbor are eliminated. (If there are one or two remaining players, then no one is eliminated.) The process repeats until either everyone is eliminated, or there is a round where no one is eliminated. An example game is shown below.

   
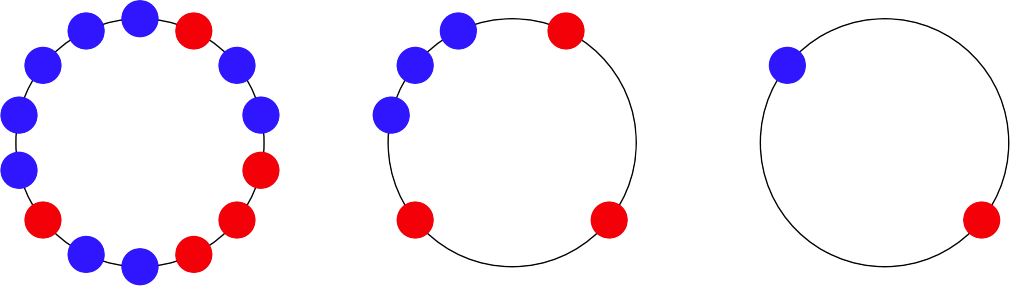
   1. For which values of n is it possible for all players to be eliminated?
   2. For those n for which it is possible for all players to be eliminated, what is the minimum number of rounds that it can take to eliminate all players (in terms of n)? What is the maximum?

2. A pentabend is the following shape (or its reflection). Its boundary is made up of five congruent arcs. Each arc is 1/6 of a circle of radius 1, so it has length π/3.

   

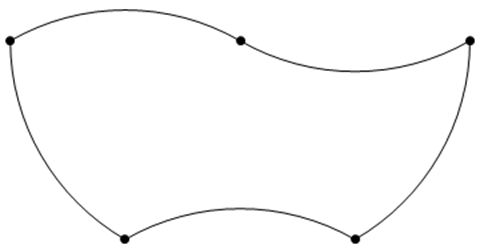
   Suppose we take X pentabends and join them, without overlap and along complete arcs only, into a bigger figure whose boundary has length Y. Then this figure is said to have roundness X/Y.

   What is the maximum possible roundness of such a figure? You should find the best lower and upper bounds you can (the largest roundness of any figure you can find, and the smallest value that you can prove can never be exceeded) even if they do not meet.

3. One day, at dawn, the corner of a quarter-infinite grid of squares catches fire. Each day, firefighters choose a square that is not on fire and protect it, permanently preventing it from catching fire. Every night, the fire spreads from all the squares that are currently on fire to all orthogonally adjacent squares that are not protected. Squares already on fire remain on fire.

   1. Prove that the firefighters cannot contain the fire to a finite area.
   2. Now suppose that an m × n rectangle in the corner of the grid is initially on fire. Also suppose that on the first day, the firefighters are allowed to protect more than one square. (On subsequent days, they can still only protect one square per day.) What is the minimum number of squares that the firefighters need to protect on the first day in order be able to eventually contain the fire to a finite area?

4. Let ℤ denote the set of integers. An arithmetic sequence is a set of the form {an + b : n ∈ ℤ} with a, b ∈ ℤ and a ≠ 0.

   A set of integers is called sequential if it is a (possibly infinite or empty) union of arithmetic sequences. A set of integers is called con-sequential if its complement in ℤ is sequential.

   1. Show that an intersection of two sequential sets is sequential. Is an infinite intersection of sequential sets necessarily sequential?
   2. Show that a union of finitely many arithmetic sequences and finitely many integers is con-sequential. Does every con-sequential set have this form?
   3. Convince yourself that a finite union of arithmetic sequences is both sequential and con-sequential. Are there any other sets that are sequential and con-sequential?
5. 1. Let n and k be positive integers with k ≥ 2. Tony is trying to unlock the door to the Cookie Ferry, which is secured by a string of n digits. Each digit may be one of the values 0 through k-1, and the string originally starts off as all 0s. On every move, Tony may either increase a single digit by 1, or change a single k-1 to 0. To unlock the door, Tony must perform a sequence of moves such that each of the kⁿ possible strings appears exactly once, and such that the ending string has all of its digits equal to k-1.
      Determine, with proof, all positive integers n and k for which Tony can unlock the door. (For instance, when n=3 and k=2, this is possible because Tony can use the sequence of moves 000 → 001 → 011 → 010 → 110 → 100 → 101 → 111.)
   2. The staff are looking for a new combination for the Cookie Ferry, with n=2. If they perform a sequence of moves starting from 00, such that each of the k² strings appears exactly once, then what are the possible ending strings (in terms of k)?

6. Oh no! The campers have run away with... the staff's stash of cookies!

   A group of 15 mentors found out about this and came to try to win their cookies back. The campers decided to arrange a small game for them: each mentor will be moved to a separate room, given a box of sandwich cookies or chocolate chip cookies, and then has to guess the name of another mentor who received a box of the same type of cookies. The mentors who guess correctly get to keep their boxes of cookies, and the other boxes are taken away.

   Before being led to their separate rooms, the mentors are allowed to coordinate to formulate a strategy, but they cannot communicate after they are separated.

   How many boxes of cookies can the mentors guarantee to keep? (This is a hard question, so we'd appreciate any partial progress!)

Problems 1, 3, and 6 are by Tejo Madhavarapu (MC '25). Problem 2 is by Misha Lavrov (MC staff). Problem 4 is by Eli Gold (MC '23–'25) and Everett Guo (MC '24–'25). Problem 5 is by Tarun Rapaka (MC '24–'25).